OmniSim

Nonlinear FETD (volume chi-3): temporal solitons

Simulation of chi-3 nonlinearity using OmniSim FETD

OmniSim’s FETD engine features the capability to simulate an isotropic instantaneous Kerr chi-3 nonlinear response, concurrently with the other models of linear dispersion (Drude, Lorentz etc). Here we will show how chi-3 nonlinearity can lead to the formation of a temporal soliton, as presented in [1]. Simply put, the soliton is a propagating solution of the nonlinear field equations which maintains a localized and constant shape due to the competing influences of the linear dispersion and the nonlinear response.

The device, consisting of vacuum on the left and a nonlinear and dispersive material on the right (dark blue region).

The device consists of a 50um vacuum region followed by a region containing a material which has a linear dispersion given by a single-pole Lorentz model with an additional instantaneous Kerr chi-3 nonlinear response given by:

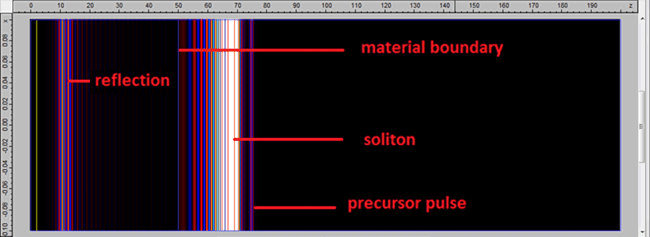
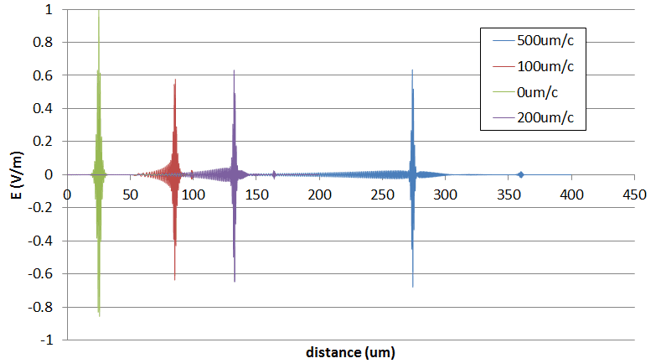
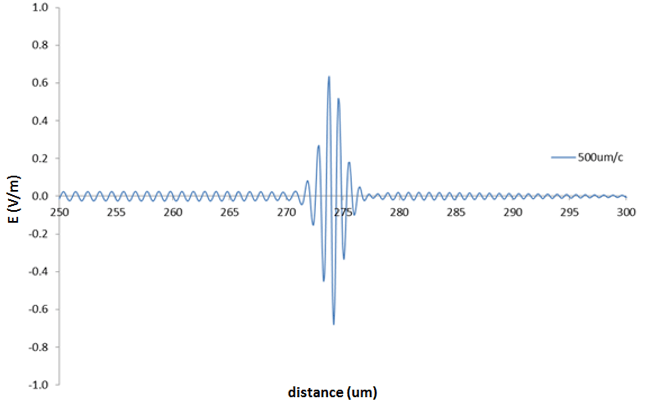
The device was excited with a right-moving initial pulse with a hyperbolic secant profile. This was allowed to propagate into the region containing the nonlinear and dispersive material and the formation of a soliton was observed. 

The electric field during the calculation.

The overall form of the propagating field shows a very close resemblance to the results illustrated in [1]. Identical results were obtained from 2D and 3D FETD simulations.  

The electric field profile at various instants during the calculation, including the initial condition (green).
Note the small high-frequency precursor pulse.

The electric field profile of the soliton after propagating for a duration of 500um/c.

References

[1] "Computational Electrodynamics: The Finite-Difference Time-Domain Method", A. Taflove, S. Hagness; Artech House. Ch.9 "Dispersive and nonlinear materials".