OmniSim

Mie scattering from a gold cylinder

Plasmonics simulated with OmniSim's FETD and FDTD software

OmniSim's FETD Engine was used to model scattering from a gold cylinder in 2D, and the results were compared with Mie scattering theory [1]. The FETD engine is an ideal tool for modelling plasmonics, particularly for difficult cases involving curved or slanted interfaces.

As a complement to the FETD calculations, we also used the FDTD engine with its Sub-Gridding tool.

When modelling Mie scattering, both FDTD and FETD provide accurate results for large wavelengths, however the accuracy of FDTD calculations deteriorates as the wavelength decreases below 4x the radius. Our FETD algorithm is ideal for the modelling of such problems and is able to obtain consistently accurate results for a much broader range of wavelengths.

(left) mesh of the FETD engine near the metal and
(right) out-of-plane H field component plotted live during the FETD calculation.

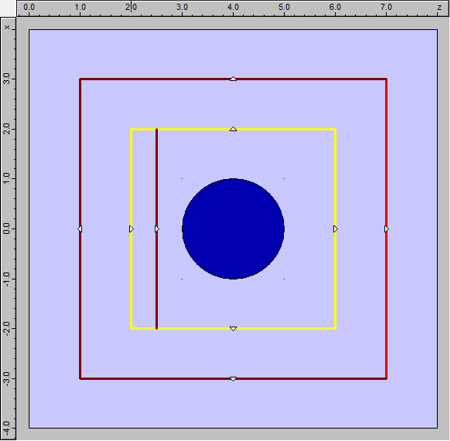
Description of the structure

The 2D structure is represented below; the blue disc corresponds to the gold scatterer and the rest of the device is filled with air.

We injected a plane wave with a broadband spectrum and we used the well known total field / scattered field approach with our FETD engine to calculate the scattering efficiency; this approach allowed us to measure scattered field with high precision, even when the scattered energy is much smaller than the input beam.

OmniSim simulation: the blue disc is the gold cylinder, the total field area is inside the yellow rectangle
and the scattered field area outside. The red lines are the sensors used to measure the input flux and the scattered flux.

We considered a radius of 1um for the gold cylinder. The FETD calculation relied on a 2D triangular adaptive mesh, which conformed to the edges of the cylinder. You can see the FETD mesh below; note how the triangles get smaller close to the metal. We used a Drude material model for modelling the dispersion in the gold region.

Mesh of the FETD engine near the metal

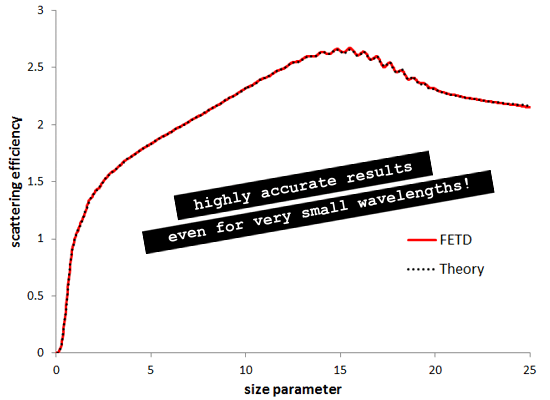
Although the FETD mesh elements are much larger than the ones that would be used for a typical FDTD calculation, the FETD engine is able to use higher order elements than FDTD, therefore allowing us to obtain a much higher accuracy for an equivalent mesh size. The adaptive mesh allows us to model the curved interface between air and gold without any sampling issues. An FDTD mesh is rectangular, which would result in a level of staircasing when modelling curved surfaces, therefore limiting the accuracy at small wavelengths.

FETD simulation results for the Mie scattering from a metal cylinder

You can see the results from the simulation in the graph below. The vertical axis gives the dimensionless scattering efficiency, which is the rate at which energy incident on the cylinder is scattered to infinity. The horizontal axis is the size parameter, which is equal to the perimeter of the disc divided by the wavelength (2*pi*R/lambda). The calculation time was 340s on a 4-core i7-860.

Scattering efficiency versus size parameter (=2*pi*R/lambda), for lambda > 0.25*R. The red curve
is FETD and the dotted black curve is obtained from the Mie theory. The accuracy of the FETD
calculation is excellent over the entire wavelength range, even at low wavelengths
(size parameter > 1.5) where the accuracy of an FDTD calculation would be poor.

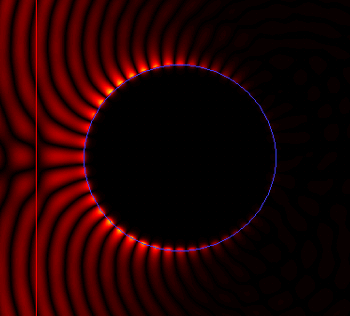
Note the excellent agreement between the FETD results and the theory over the entire range of size parameter. Obtaining good agreement for a size parameter below 1.5 is fairly easy and can be achieved routinely with an FDTD engine, as the wavelength is at least 4x larger than the radius of the cylinder. However, achieving high accuracy for smaller wavelengths is very challenging for FDTD. Here we consider wavelengths as low as 0.25x the radius. Tests perform with an FDTD engine show that in that range the FDTD method struggles to get close to the theory, despite much longer calculation times.

With OmniSim you can plot the field evolving live during FETD and FDTD calculations. You can find below a picture of the magnetic field profile obtained with the FETD engine, showing the low wavelength scattering pattern. Note the remarkable symmetry, as well as the pattern of the surface plasmons propagating along the curved surface.

Hy field profile (out-of-plane component) taken from the FETD calculation.

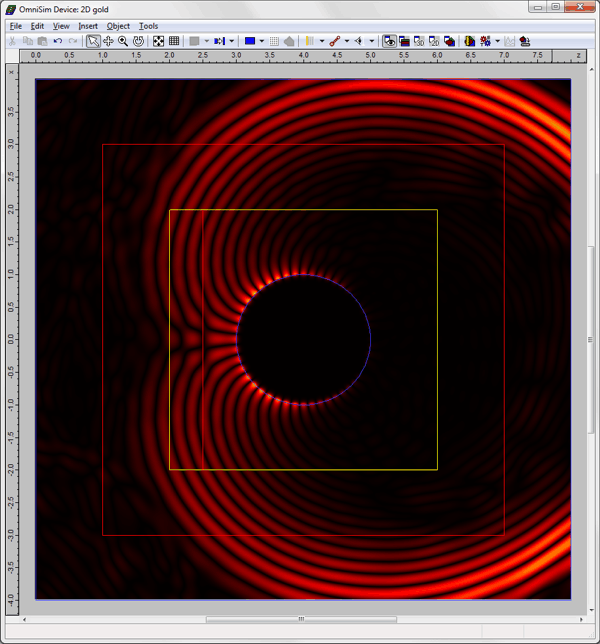
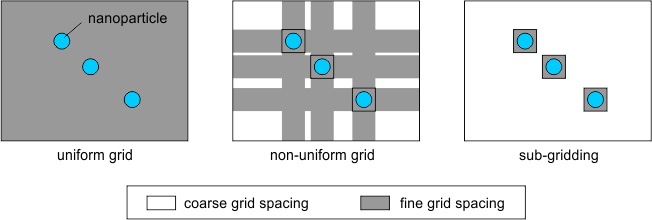
Mie scattering modelled with the FDTD Sub-Gridding tool

FETD is by far the most accurate and efficient method for the modelling of nano-particles and curved metal interfaces (see Mie scattering example above), however it is still possible to use the FDTD method in some cases.

The main challenge when modelling plasmonics is that the grid spacing needs to be very fine near the surface of the metal, although it can be much coarser in other parts of the structure. OmniSim's FDTD Engine features a unique FDTD Sub-Gridding tool which allows you to increase the spatial resolution locally, only where it is needed, reducing the simulation time considerably with respect to a uniform or even a non-uniform grid.

Surface plasmons on gold nano-particle, exhibiting 8x finer resolution in the subgrid region.

The FDTD Sub-Gridding tool allows you to reduce the simulation time considerably with respect to a uniform or even a non-uniform FDTD grid.

Benefits of sub-gridding against uniform and non-uniform grids.

Reference

[1] M. Born and E. Wolf, "Principles of Optics", 7th edition, Cambridge University Press (1999)