FIMMPROP

Taper Modelling

Modelling tapers and continuously varying structures with FIMMPROP

FIMMPROP allows you to model propagation in z-varying sections, as can be commonly found in tapers, directional couplers, Y-junctions etc. This is done by discretising such sections along the axis of propagation and calculating the local modes along the taper.

FIMMPROP can model tapers of arbitrary length and complexity more efficiently than most simulation tools and it can sweep design parameters very efficiently; for instance scanning the length of a tapered waveguide is quasi-instantaneous.

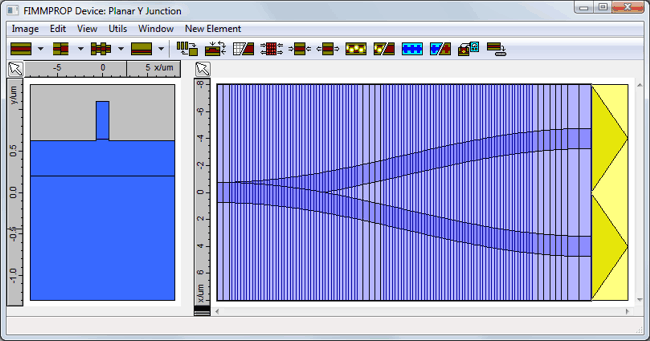
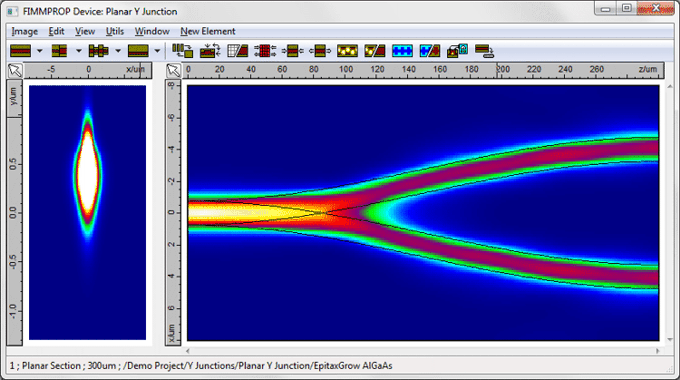
A unique adaptive taper algorithm

FIMMPROP includes a unique adaptive taper algorithm, which can refine the discretisation dynamically depending on the variations of the eigenmodes.

For instance in the planar Y-junction shown below, the discretisation needs to be much finer in the region where the waveguide widens than in other parts of the structure, where the width of the waveguide remains constant. Attempting to model this taper with a constant-step taper algorithm would be very inefficient, as to obtain the same accuracy you would need to apply the finest discretisation everywhere.

Discretisation of Y-junction by the taper algorithm, showing the adaptive discretisation step.
The discretisation is finest around 30% of the length of the taper, where the modes undergo
strong changes due to the widening of the rib waveguide.

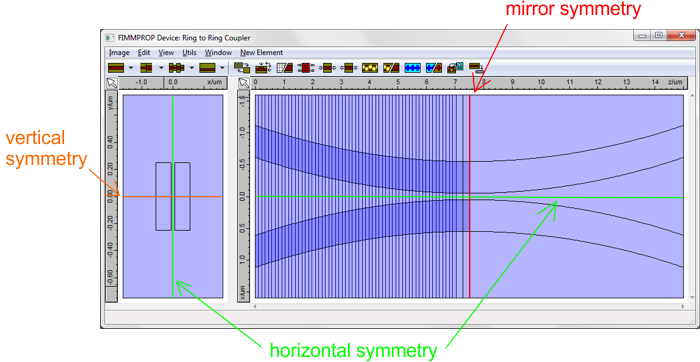
Photon Design has a well established expertise in the modelling of such structures, and pioneered the development of methods for the modelling of tapers and z-varying structures with EME by publishing articles on the subject as early as 2003 [1].

Taking advantage of symmetries

Many tapered structures include one or two planes of symmetry, and other structures like ring couplers or directional couplers include mirror symmetries. FIMMPROP can take advantage of such symmetries when modelling tapers, reducing calculation time by up to 16x compared with an algorithm that would not account for such symmetries.

Ring to ring coupler; here FIMMPROP can take advantage of the horizontal (green line)
and vertical symmetries (orange line) of the waveguide cross-section,
aand of the mirror symmetry (red line) of the layout.

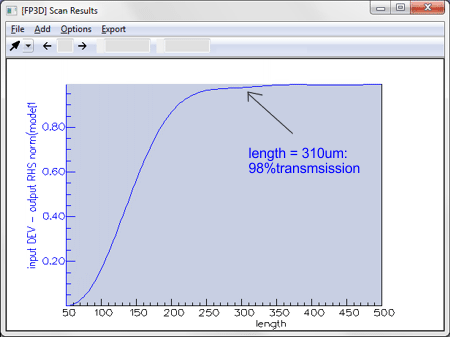
For tapered fibers, FIMMPROP can even take advantage of the cylindrical symmetry of the structure through the use of fiber solvers, making calculations extremely fast.

Instantaneous taper length scans

Once the scattering matrix for the taper has been calculated, FIMMPROP is able to vary some parameters very quickly using the FIMMPROP Scanner or using scripts. In most cases varying the length of a taper can be done almost instantly. This allows you to optimise the length of the taper at a very low cost in calculation time.

For instance in the Y-junction shown above, the initial calculation of the scattering matrix took 110s. Once this was calculated, the transmission versus length scan below only took 0.2 seconds per step.

Transmission vs taper length calculated with the FIMMPROP Scanner for the Y-junction shown above.

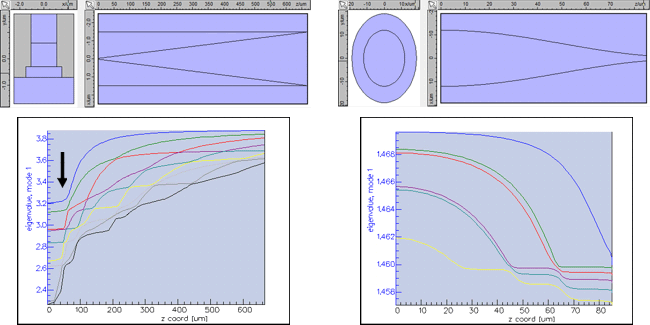
Benefits of modal analysis

FIMMPROP can help you understand the physics of your taper in more detail than any other tool:

• FIMMPROP can plot the evolution of the power in each mode along the taper, allowing you to guarantee single mode behaviour by detecting coupling to high order modes or by engineering high losses for high order modes.

• FIMMPROP allows you to study the variations of the mode properties along the taper: effective indices, mode losses, mode polarisation, mode size, confinement factor etc. Designers can take advantage of this information to identify geometries which will give the most compact adiabatic tapers, as shown in the example below.

Two different taper geometries with the evolution of the effective indices
with Z for the first few modes plotted underneath.

(left) Planar geometry: plotting the effective indices versus Z reveals an anti-crossing (pointed by the arrow)
for the fundamental mode (blue). The anti-crossing will be associated with mode coupling
and potential losses and it will be difficult to make such a taper adiabatic.

(right) Fiber geometry: in this case there is no anti-crossing for the fundamental mode (blue),
meaning that it should be possible to make this taper adiabatic even for a short taper length.

Case studies

You can find below a few examples of applications taking advantage of FIMMPROP's taper algorithm.

Planar geometry:

Inverted Planar Taper (SOI)

Planar Y-junction

Microring Coupler

Optimize Taper Designs (with Kallistos)

Optimize S-Bends (with Kallistos)  

Fibre geometry:

Tapered Fibre Filter

Tapered Metal-coated SNOM Fibre Probe

Lensed Fibre

Reference

[1] D. F. G. Gallagher, T. P. Felici, "Eigenmode expansion methods for simulation of optical propagation in photonics: pros and cons", Proc. SPIE 4987, Integrated Optics: Devices, Materials, and Technologies VII, 69 (2003) - PDF