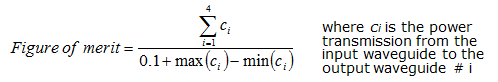FIMMPROP

SOI 1x4 MMI Coupler Optimisation

3D simulation and optimisation in silicon photonics with FIMMPROP and Kallistos

In this example we combine FIMMPROP with our optimisation tool Kallistos to optimise a 1x4 MMI coupler in rigorous fully vectorial 3D for silicon photonics, based on an SOI buried waveguide geometry.

Kallistos can take advantage of FIMMPROP's ability to scan design parameters very quickly, allowing us to investigate an extremely large number of structures in a small amount of time: on average we were able to investigate 8.3 designs per second!

Although we focused on a silicon 1x4 MMI coupler, the same approach can be applied to any MMI design with any number of input and output branches.

Optimised 1x4 MMI coupler based on a buried silicon waveguide geometry

Benefits of using FIMMPROP to model MMI couplers

EME (EigenMode Expansion) is the ideal method to model MMI couplers. The physics of MMIs results from constructive and destructive interferences between a small number of guided modes; it is these interferences that give MMIs their ability to generate multiple images of the input beam. EME is a mode-based approach, and it therefore offers an extremely efficient way of modelling such devices.

The implementation of EME in FIMMPROP offers an optimal framework for this application, with a potential for highly efficient optimisation and fully vectorial solutions:

• FIMMPROP allows you to simulate the structure with a minimal amount of calculation: you only need to calculate three sets of modes and their overlaps at two joints.
• FIMMPROP will model the structure in a fully vectorial way, allowing you to model MMIs designed in SOI (silicon-on-insulator) or other high index contrast technologies.
• FIMMPROP allows you to optimise an MMI coupler with great efficiency: when a parameter is varied with a scanner or an optimiser, FIMMPROP will only recalculate what is needed thanks to its automatic update scheme. The length of the central section can for instance be scanned almost instantaneously. Our optimiser took advantage of this at every stage of the optimisation.
• The fully bidirectional algorithm will account for all internal reflections and will allow you to simulate the structure simultaneously in both directions.

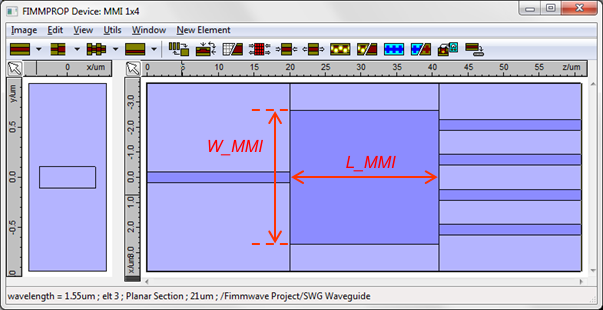
Design and parameterisation of the MMI design

We used a buried SOI waveguide geometry with a fixed silicon layer thickness of 220nm. We worked at a wavelength of 1.55um and used a refractive index of 3.5 for silicon and 1.44 for silica.

We designed the MMI coupler using FIMMPROP's user interface. We used three variables to parameterise the structure: L_MMI and W_MMI to define the length and width of the central section, and a parameter alpha_out to control the gap between the output waveguides, expressed as a fraction of the width of the MMI.

Schematic view of the MMI Coupler in FIMMPROP with the length and width of the MMI section parameterised

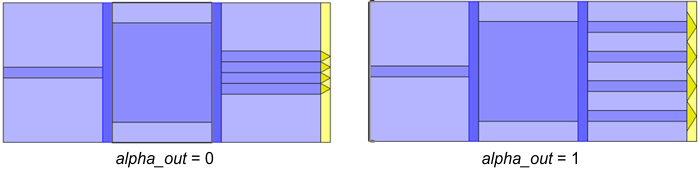
You can see below how the parameter alpha_out works: if alpha_out is set to zero the gap is zero, if alpha_out is set to 1 the gap is maximised.

Figure of merit for the optimisation

Our optimal design should provide us with low loss and a low imbalance between the power in the different output waveguides, so we asked Kallistos to look for designs that maximised the figure of merit shown below.

The optimiser was set up to vary the W_MMI and alpha_out. At each step of the optimisation, we got Kallistos to run a Python script which scanned the length of the MMI coupler and returned the optimal length for the selected values of W_MMI and alpha_out. Kallistos's ability to combine an optimiser with a script allowed us to run an optimisation with a very high level of complexity.

As FIMMPROP can scan the length of a section instantly, this allowed us to obtain a much more efficient and finer optimisation than if we had included the length of the MMI in the optimisation settings.

Preliminary studies

Ideal dimensions of input and output waveguides

We used FIMMWAVE's Waveguide Scanner to study the effect of waveguide width on the effective index of the first order mode and found that the largest width to allow single-mode behaviour is 420nm. Such a small waveguide width leads to significant insertion losses, and we decided to use a larger width for the input and output waveguides. We will taper the waveguides to vary the waveguide width from the input and output waveguides to the single core waveguides used in the rest of the circuit.

After a preliminary study we decided to set the width of the input and output waveguides to 1.5um, as this allowed us to keep insertion losses below 0.1dB.

Minimum gap between output waveguides

We then studied how large a gap we needed in between two output waveguides to minimise cross-coupling: we need to ensure that the cross-coupling is sufficiently low to permit the introduction of adiabatic tapers and the separation of the waveguides.

Here again we used the Waveguide Scanner for a structure with two-branches and we studied the effect of the gap on the coupling length. We found that a gap of 0.15um between two branches gave a coupling length of 1mm, which we assumed would be sufficient.

From this preliminary study we have established the following constraints on our design.

Performance of the optimiser

On a 8-core Xeon E5620 the optimiser calculated 29 iterations per hour; the modes were calculated semi-analytically with the FMM Solver. The SOI waveguide has a high index contrast and we generated mode profiles with a very high-resolution to calculate the overlaps with precision.

At each iteration of the optimiser, Kallistos ran a script which controlled a FIMMPROP Scanner varying the length of the MMI coupler. The script ran a first scan of 512 different lengths with a step of 100nm and identified the optimum length; it then ran a second finer scan around the optimum to refine the results.

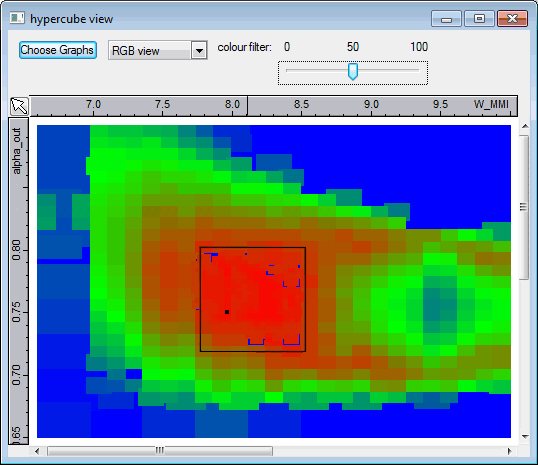
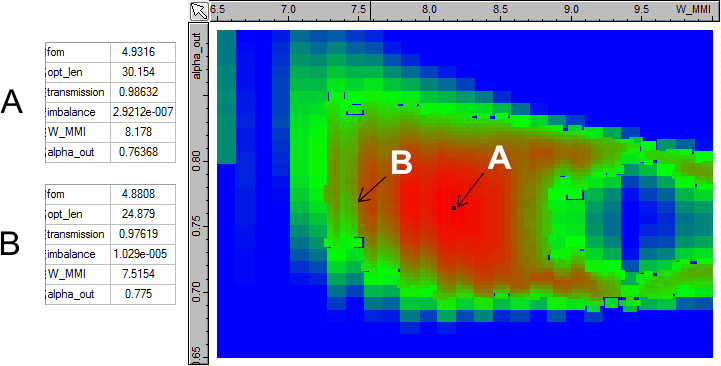
Combine the optimiser with a script allowed us to study over 712,700 structures in 24 hours: an average of 8.3 designs investigated per second, with a rigorous 3D fully vectorial approach!

Exploring the optimisation results

Kallistos allows you to visualise the optimisation data during the optimisation, and you can decide to pause and restart the optimiser in order to investigate the results and decide whether you want to push the optimisation further.

You can see for instance what the optimisation data looked like after a first overnight run. The data is shown as calculation points on a map of the parameter space, with the width of the MMI W_MMI plotted in microns along the horizontal axis and the waveguide spacing parameter alpha_out plotted along the vertical axis.

From this plot it is clear that we can narrow down the region of interest in the parameter space to the zone that we have delineated by a black line, in which the optimal results seem to be concentrated.

Colour map of the optimisation results

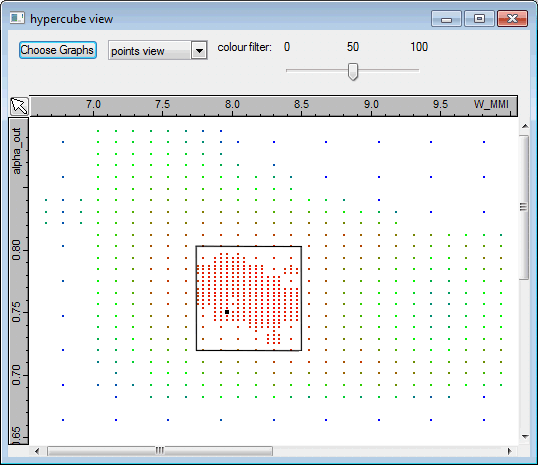
You can see here the same data, with each calculation point shown individually; as you can see the optimiser has already focused most of its efforts in the region that we have identified.

Point view of the optimisation data

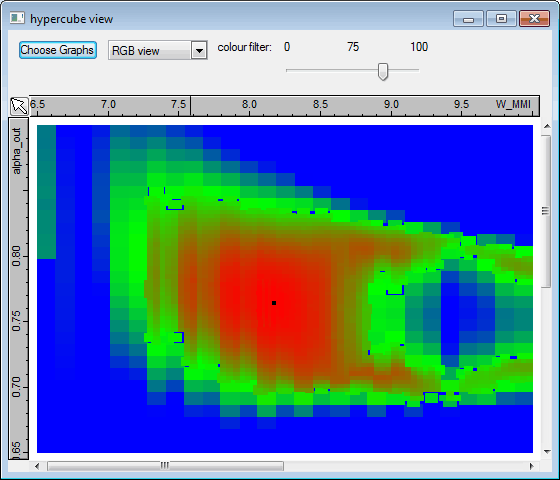
We decided to let the optimiser run for a little longer and this is the data that we eventually obtained.

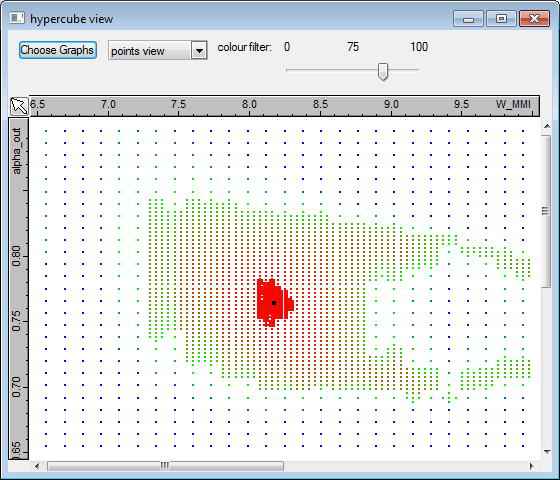
You can see in the graph below the position of the global optimum "A" in the optimisation space, at the centre of the optimum region. The properties and performance are shown on the left-hand side; "fom" is the figure of merit, "opt_len" is the optimal length of the MMI in microns, "transmission" is the sum of the power coupled to the four output waveguides and "imbalance" is the maximum discrepancy between the power in two output waveguides divided by the average output power.

Design "A" corresponds to an optimum MMI length of 30.1um. As Kallistos allows us to visualise and post-process all the optimisation data we decided to look for the best design to allow us to keep the MMI length below 25um. The resulting design is shown below as design "B"; the imbalance is almost as good as design "A" but the total transmission dropped by 1%.

Optimal designs: A is the global optimum, B offers an alternative for an MMI length below 25um

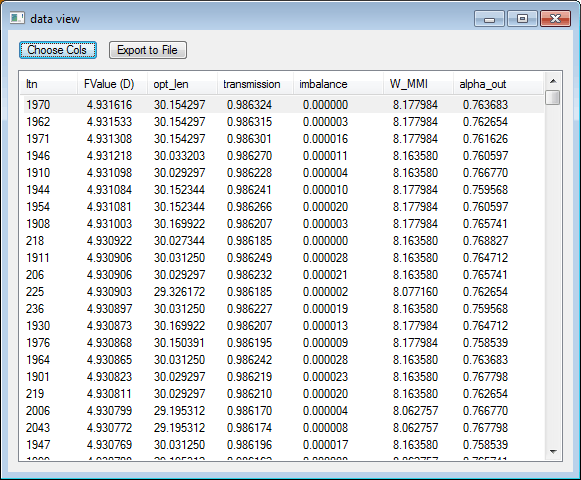
Kallistos is a fully transparent tool and you can inspect the data associated with each optimisation data point, allowing you to browse the raw data in order to find optima that correspond to your own criteria. For instance a global optimum might be located on the edge of a high-performance region, but you might choose as an optimal design a point located nearer the centre of the region in order to give you a better fabrication tolerance.

Raw numerical data obtained from the optimiser

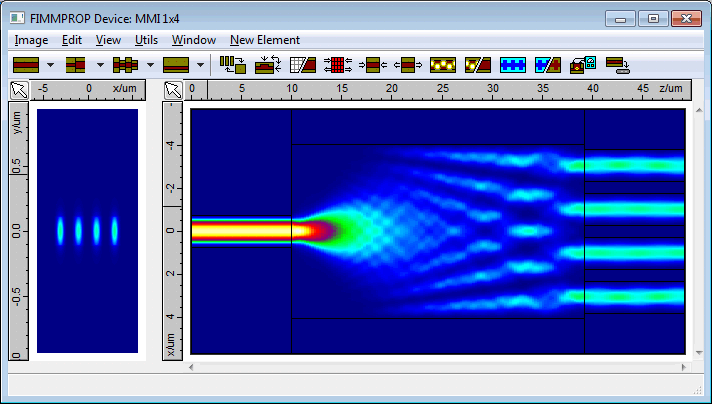
Performance of the optimal structures

We used FIMMPROP to simulate the optimal designs that we identified from the Kallistos optimisation. You can see below the intensity profile for design A. The total loss is 0.060dB and the variation in power between the output waveguides is less than 0.00003% i.e. negligible.

Intensity profile for design "A"