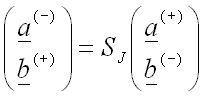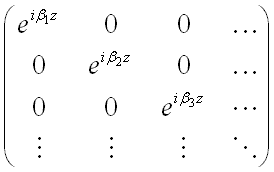|
Your source of photonics CAD tools | |
|
| ||
FIMMPROPA bi-directional optical propagation tool |
   |
EigenMode Expansion (EME)A rigorous method for modelling optical propagationBi-directional simulation of light propagation based on EigenMode Expansion (EME) as implemented in FIMMPROP is an innovative technique which allows you to model a very wide range of structures with a level of accuracy that methods such as FDTD, BPM or FEM cannot attain. Here we will discuss EME, the method on which FIMMPROP is built. This introduction is not necessary to understand how FIMMPROP works but it will give you an insight into the underlying theory.
The EME technique has been well established in photonics for some time. It is a very simple technique in essence. Key principles of eigenmode expansionTo understand how EME works, we must start with a definition of the "mode" or "eigenmode" of a waveguide.
In a structure where the optical refractive index does not vary in the z direction, we find solutions of Maxwell’s Equations of the form
We assume here a single wavelength and time
dependence of the form
Mathematically
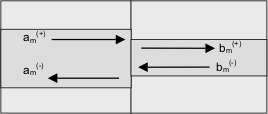
In a typical waveguide, there are a few guided modes (which propagate without loss along the waveguide), but in addition there is an infinite number of radiation modes (which carry optical power away from the waveguide). Since we cannot efficiently deal with an infinite number of radiation modes we surround the structure by boundaries which will cause the radiation modes to become a discrete set (we will deal with reflections off these boundaries later). The guided and discretised radiation modes together form a complete basis set – in other words we can express any solution of Maxwell’s Equations in the region of the waveguide in terms of a superposition of the forward and backward propagating modes:
where
This set of equations is an exact solution of Maxwell’s Equations in a linear medium, assuming an infinite sum. In practise we can truncate the sum to a finite basis set and still maintain high accuracy. The size of the set needed will depend on the problem, with more modes needed to model light travelling at a large angle to z. Modelling discontinuitiesSo far we have a technique for analysing only z-invariant structures. Next we introduce a join between two waveguides.
Maxwell’s Equations continuity conditions for the fields allow us to deduce a relationship between the coefficients of the form:
where SJ is a scattering matrix for the join. The scattering matrix expresses the fields travelling away from the join in terms of the fields incident on the join. Having an expansion in terms of a complete set of modes permits to write a scattering matrix for any component. The scattering matrix SWG for a straight section is simply: which is clearly trivial to compute once the eigenmodes have been found. Key featuresThese few equations immediately illustrate some useful features of EME: - it is fully bi-directional; in fact it can be made omni-directional if sufficient modes are used. - it is a fully vectorial algorithm, making no approximations about the light polarisation. - it is a rigorous solution to Maxwell’s Equations; the main approximation being the finite number of modes used. The scattering matrix approach means that you solve the problem for all inputs simultaneously, so you can for example get the response for both TE and TM polarisations in one go. It also allows you to divide a large circuit into multiple parts and then re-use the s-matrix of the parts again potentially saving a lot of time. It allows efficient modelling of periodic or repeating structures since one can evaluate the s-matrix of one period and then re-use it. Further reading
|
. 
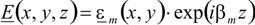
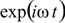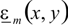and bm
are the eigenfunction and eigenvalue of the solution. So a mode has a
very simple harmonic z-dependence – this simple z-dependence is the key
to enabling EME to solve long slowly varying structures quickly and
efficiently.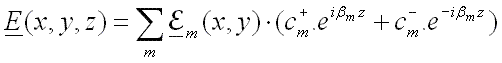
,
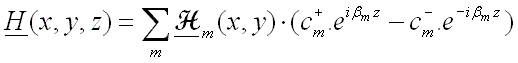
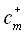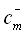are the amplitudes of the mode in the +z and –z directions respectively.
 © 2023 Photon Design copyright all rights reserved |
 |